Cinemática

La cinemática es la ciencias que estudia los tipos de movimientos sin preguntarse las causas que producen tales movimientos. Se debe hacer notar, que en gran parte la física que se propone, según los planes de estudio del Ministerio de Educación, son término de física puntal. O sea un piedra que cae desde una altura es considerada como un punto, no interesa su dimensiones ni su forma. Toda la masa está concentrada en un punto.

---

DEFINICIONES BÁSICAS

OBSERVADOR: También llamado sistemas de referencia o marco de referencia, se define en términos de la mecánica clásica, como el lugar geométrico del espacio, donde se ubica un plano cartesiano, por lo general, el cual tiene un espacio-tiempo determinado.
En general todo movimiento es relativo, y deberá siempre estar referido a otro cuerpo. Por ejemplo nosotros estamos en reposo con respecto al pc, sin embargo, con respecto al sol nos estamos moviendo.
Para estudiar el movimiento siempre nuestro sistema de referencia estará en reposo o con velocidad constante, y usaremos un sistema de coordenadas cartesianas para cuantificar el movimiento del cuerpo. Los sistemas de referencia utilizados cotidianamente cumplen las siguientes características:

• Son independientes del movimiento del cuerpo, en otras palabras el observador no altera al cuerpo en movimiento.
• El tiempo, es absoluto (es igual para cualquier observador del fenómeno)
• Las ecuaciones que rigen el movimiento de un cuerpo se cumplen equivalentemente, cualquiera sea el sistema que se observe.

POSICIÓN: Es una magnitud vectorial que se mide en unidades de longitud y corresponde al lugar geométrico- espacial que tiene el cuerpo en un instante dado. En la Fig.1 se obser

va el vector posición inicial para el cuerpo como también la final. Cabe destacar que para distintos observadores la posición del cuerpo es distinta para cada uno. Ejemplo: La posición de un barco en el puerto de Valparaíso puede se distinta dependiendo del muelle desde la cual se mide. Así para un observador ubicado en el muelle Prat, se verá que el barco hasta al norte, sin embargo desde el muelle Barón, se verá que el cuerpo esta al Noreste.

MOVIMIENTO: Un cuerpo se mueve cuando, la posición de la partícula cambia con respecto a un observador o sistema de referencia.
Por ejemplo, se puede considerar que una bola que está rodando sobre una cubierta de un barco en movimiento, efectúa un movimiento compuesto respecto de la costa; este movimiento resulta de la composición del rodamiento respecto de la cubierta, que constituye el referencial móvil, y del movimiento de la cubierta respecto de la costa.

TRAYECTORIA: Es la línea que une todas las posiciones barrida por el cuerpo. Se puede clasificar en curvilíneas y rectilíneas. La trayectoria en la Fig.1 es la curva que va desde el punto A hasta el B.

DISTANCIA: Corresponde a la longitud de la trayectoria. También es conocida como camino recorrido. En la fig.1 está dado por la longitud de la curva que une los puntos A y B. Es una magnitud escalar y se mide en unidades de longitud. Fig. 1

DESPLAZAMIENTO: Es una magnitud vectorial y se mide en unidades de longitud. Corresponde a la resta vectorial de la posición final de un cuerpo menos la posición inicial. Se obtiene que mientras más juntos estén el vector posición inicial y final, más exacto será.

Como se puede observar en la figura anterior, mientras menos es el tiempo de variación de la posición, más junto están el vector posición final y el inicial, ajustandose más a las trayectoria seguida por el cuerpo. Por lo tanto en el límite cuando el desplazamiento es infinitesimal se ajusta perfectamente a la trayectoria y la distancia que es la longitud de la trayectoria, puede aproximarse al módulo del vector desplazamiento

y el módulo del vector desplazamiento esta dado por:

El desplazamiento es resultado de una resta vectorial entre la posición final y la inicial, y no simplemene una resta algebraica o aritmética. Por lo tanto debe considerarse las reglas para restar vectores tanto de manera geométrica como algebraica sumando o restando cada componente según corresponda.
El módulo del vector desplazamiento se calcula a partir de las dos componentes resultantes del vector desplazamiento, aplicando simplemente pitágoras.

Cuando analizamos el movimiento en una dimensión, generalmente tendemos a confundir el desplazamiento, con la trayectoria y con la distancia o camino recorrido. En el siguiente esquema se muestra la diferencia de cada una.

en el esquema tenemos que:

• La posición inicial de la bolita es xo=1i (m), el vector unitario i, nos indica que esta a la derecha del sistema de referencia.
• La posición final de la bolita es xf=2 i (m), el vector unitario i, nos indica que está a la derecha del sistema de referencia.
• El desplazamiento es Δr= 1i (m), lo que quiere decir que el cuerpo se desplazó hacia la derecha 1 metro.
• Si queremos calcular la distancia, debemos pensar en la longitud de la trayectoria, la cual para este caso es una linea recta, por lo que coincide con el módulo del vector desplazamiento y vale d = 1 m, y como es un escalar no se indica la dirección (+x o -x)

---

VELOCIDAD

VELOCIDAD: Es una magnitud de tipo vectorial, que se mide en unidades de longitud dividida en unidades de tiempo, son ejemplos de unidades de medidas km/hr, m/s, cm/s...etc.
VELOCIDAD PROMEDIO Y VELOCIDAD INSTANTÁNEA: La velocidad media se define como el desplazamiento (cambio de posición) dividido en intervalo de tiempo. En si la velocidad de un cuerpo puede cambiar durante un intervalo de tiempo grande, sin embargo en la medida que se hace más pequeño el intervalo de tiempo, más se aproxima el desplazamiento a la trayectoria seguida ( Fig.3) si el intervalo es muy, pero muy cercano a cero a ese resultado que resulta de la derivada de la posición con respecto al tiempo se conoce como velocidad instantánea. Al módulo de la velocidad instantánea se conoce con el nombre de rapidez instantánea. La velocidad media se calcula realizando la diferencia de los vectores posición y luego dividiendo la magnitud en el intervalo de tiempo. Sin embargo la resta es de tipo vectorial, por lo tanto debemos considerar las dirección y sentido. Como este es un curso básico de física la velocidad en cada uno de los ejes de coordenadas será la variación de la posición en el eje correspondiente.

LA RAPIDEZ MEDIA: Relaciona la distancia total recorrida y el tiempo que tarda en recorrerla. No se debe olvidar que se mide en unidades de longitud por unidad de tiempo (L/T) y que la rapidez es una magnitud escalar.

Hablar de rapidez y velocidad físicamente no es lo mismo y esto lo podemos demostrar con las siguientes relaciones matemáticas:

---

ACELERACIÓN

ACELERACIÓN MEDIA: Se define como el cambio de la velocidad media con respecto al tiempo. Cuando hablamos de un cambio en el vector velocidad nos referimos tanto al módulo, sentido y dirección. Ejemplo: Si un cuerpo describe una trayectoria circular siempre demorando el mismo tiempo en completar una vuelta, el módulo del vector velocidad no cambia,sin embargo la dirección y sentido lo hacen continuamente, por lo tanto debe existir una aceleración, y esa se llama aceleración media centrípeta.

---

MOVIMIENTO RECTIĹINEO UNIFORME

• El movimiento es uniforme si la velocidad (que veremos ahora) es siempre la misma, es decir, si la velocidad es constante.
  Si no es uniforme, el movimiento es acelerado (aunque la aceleración puede ser uniforme, o sea, constante).
• Velocidad:
  La velocidad es el espacio recorrido por unidad de tiempo. En otras palabras, lacantidad de espacio que se recorre en un tiempo determinado.
  En un movimiento rectilíneo uniforme, la velocidad es
  
  $$v=\frac{x}{t}$$
  donde v es la velocidad, x la distancia o espacio recorrido y t el tiempo necesario para recorrer la distancia x.
  su unidad de medida en el Sistema Internacional es el metro por segundo, m/s. Esto es, el recorrido o espacio se mide en metros y el tiempo en segundos.
  La velocidad es directamente proporcional al espacio recorrido e inversamente proporcional al tiempo, lo que quiere decir que, fijado el tiempo t, cuanto mayor es la velocidad, mayor es la distancia recorrida; o bien, fijada la distancia recorrida, cuanto menor es el tiempo, mayor es la velocidad.
• Gráfica v(t): velocidad en función del tiempo
  La siguiente gráfica muestra la velocidad de dos móviles: un móvil que se mueve de forma uniforme y otro que se mueve de forma acelerada.
  
  
  Según esta gráfica, el móvil A, con movimiento uniforme tiene una velocidad constante de 2m/s por lo que su gráfica es una recta horizontal.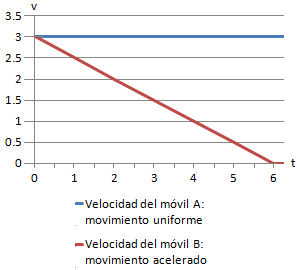
  Si la gráfica de v(t) no es una recta horizontal, el movimiento no es rectilíneo uniforme.
  En el movimiento acelerado del otro móvil, B, la velocidad no es constante, sino que va decreciendo hasta llegar a 0, es decir, hasta que el móvil se detiene en el tiempo t = 6s.
  En el movimiento rectilíneo uniforme (velocidad constante), la gráfica v(t) siempre es una recta horizontal.
  Si consideremos el rectángulo que forma la gráfica v(t)
  
  
  Sus lados son: la base es el tiempo transcurrido, t; y la altura es la velocidad, v(t). El área del rectángulo es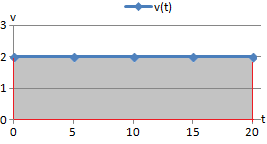
  
  $$área=v\cdot t$$
  Y sabemos que el espacio recorrido es la velocidad por el tiempo. Por tanto, el área del rectángulo es el espacio recorrido.
• Gráfica x(t): distancia en función del tiempo
  La siguiente gráfica muestra el espacio recorrido por dos movimientos rectilíneos uniformes: el del móvil A, con velocidad 5km/h; y el del móvil B, con velocidad 7km/h.
  
  
  Podemos observar que en ambos casos la gráfica x(t) es una recta no horizontal. Esto se debe a que la ecuación de la distancia es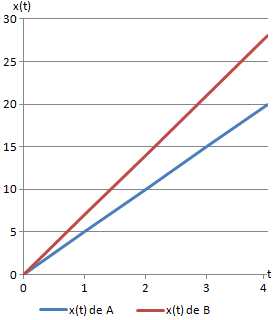
  
  $$x=v\cdot t$$
  siendo v una constante.
  La pendiente de la recta depende del valor de la velocidad v. Cuando mayor es v, más rápido crece la recta. Por esta razón, la pendiente de la gráfica del móvil B es mayor que la del móvil A.
  Este hecho es bastante lógico puesto que la gráfica indica la distancia recorrida y, por tanto, cuando mayor sea la velocidad, mayor es la distancia recorrida.
  Si la gráfica x(t) no es una recta, el movimiento no es rectilíneo uniforme

PROBLEMAS RESUELTOS

Problema 1. Un camión se mueve a velocidad constante de 90km/h por una autopista recta.

A. ¿Qué distancia recorre en 2 horas?

B. ¿Qué distancia recorre por segundo?

C. ¿Cuánto tardará en recorrer 10km?

Solución

Apartado a:

La ecuación del movimiento es

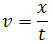
donde conocemos la velocidad y el tiempo. Queremos obtener la distancia recorrida: aislamos la x antes de sustituir en la ecuación:

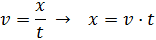
Ahora sustituimos los datos

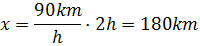
Hemos escrito las unidades de tiempo para tratarlas como factores, de este modo, como el tiempo, h, está multiplicando y dividiendo, desaparece, quedando únicamente la unidad de distancia, km.

Por tanto, el camión recorre 180 kilómetros en 2 horas.

Apartado b:

De nuevo tenemos que calcular la distancia, pero ahora, en un tiempo de 1 segundo.

Sabemos que la distancia recorrida es

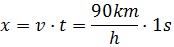
Notemos que en el denominador tenemos el tiempo en horas y en el numerador en segundos. Necesitamos la misma unidad. Para ello, pasaremos las horas a segundos.

Una hora son

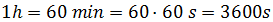
Entonces, escribimos 3600s donde tenemos la h:

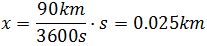
Como las unidades del tiempo son la misma, se han anulado.

El espacio recorrido obtenido está en kilómetros, por lo que si queremos evitar los decimales podemos pasarlo a metros:

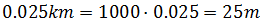
Por tanto, el camión recorre 25 metros cada segundo.

Apartado c:

Ahora sabemos la distancia, x = 10km , y tenemos que calcular el tiempo. Aislamos el tiempo en la ecuación:

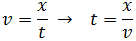
y sustituimos los datos

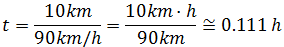
Notemos que las horas están dividiendo en el denominador, por lo que pasan multiplicando al numerador.

Escribimos el tiempo en minutos para evitar los decimales:

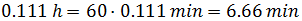
Para ser más exactos,

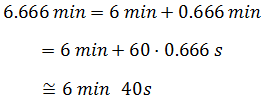
Por tanto, el camión tarda unos 6 minutos y 40 segundos en recorrer 10km.

Problema 2. La velocidad de la luz en el vacío es c = 300 000 km/s. La luz del Sol tarda en llegar a la Tierra 8 minutos y 19 segundos. Calcular la distancia entre el Sol y la Tierra.

Solución

La velocidad la hemos llamado c en vez de v ya que para la luz se utiliza este nombre, pero el procedimiento es el mismo.
Por tanto, conocemos la velocidad, c, y el tiempo, t = 8 min 19s. Podemos calcular la distancia:

Antes de sustituir tenemos que expresar el tiempo en una sola unidad. Como la velocidad la tenemos en kilómetros por segundo, pasamos el tiempo a segundos:
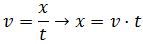
Por un lado, los 8 minutos son

Por tanto, el tiempo es

Ahora sustituimos los datos en la ecuación:

Por tanto, la distancia del Sol a la Tierra es de 149 700 000km, es decir, casi 150 millones de kilómetros.

---

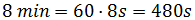
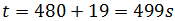
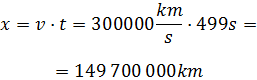
MOVIMIENTO RECTIĹINEO UNIFORMEMENTE ACELERADO

Un movimiento rectilíneo uniformemente acelerado es un tipo de movimiento frecuente en la naturaleza. Una bola que rueda por un plano inclinado o una piedra que cae en el vacío desde lo alto de un edificio son cuerpos que se mueven ganando velocidad con el tiempo de un modo aproximadamente uniforme; es decir, con una aceleración constante.

Este es el significado del movimiento uniformemente acelerado , el cual “en tiempos iguales, adquiere iguales incrementos de rapidez”.

En este tipo de movimiento sobre la partícula u objeto actúa una fuerza que puede ser externa o interna.

En este movimiento la velocidad es variable , nunca permanece constante; lo que si es constante es la aceleración.

Entenderemos como aceleración la variación de la velocidad con respecto al tiempo . Pudiendo ser este cambio en la magnitud (rapidez) , en la dirección o en ambos.

Las variables que entran en juego (con sus respectivas unidades de medida) al estudiar este tipo de movimiento son:

Velocidad inicial           Vo (m/s)

Velocidad final              Vf  (m/s)

Aceleración                     a  (m/s 2 )

Tiempo                             t   (s)

Distancia                         d  (m)

Para efectuar  cálculos que permitan resolver problemas usaremos las siguientes fórmulas:

Consejos o datos para resolver problemas
La primera condición será obtener los valores numéricos de tres de las cinco variables . Definir la ecuación que refleje esas tres variables. Despejar y resolver numéricamente la variable desconocida.

Tener cuidado con que en algunas ocasiones un dato puede venir disfrazado; por ejemplo:

"un móvil que parte del reposo.....", significa que su velocidad inicial es Vo = 0 ; "en una prueba de frenado...", significa que su velocidad final es Vf = 0 .

Veamos un problema como ejemplo

En dirección hacia el sur, un tren viaja inicialmente a 16m/s; si recibe una aceleración constante de 2 m/s 2 . ¿Qué tan lejos llegará al cabo de 20 s.? ¿Cuál será su velocidad final en el mismo tiempo?

Veamos los datos que tenemos:

Conocemos tres de las cinco variables, entonces, apliquemos  las  fórmulas:

Averigüemos primero la distancia que recorrerá durante los 20 segundos:

Conozcamos ahora la velocidad final del tren, transcurridos los 20 segundos:

Respuestas:

Si nuestro tren, que viaja a 16 m/s, es acelerado a 2 m/s recorrerá 720 metros durante 20 segundos y alcanzará una velocidad de 56 m/s.