Cantidades Vectoriales
Las magnitudes físicas o variables se clasifican en dos grandes grupos:
Las escalares: Son aquellas que quedan definidas exclusivamente por un módulo, es decir, por un número acompañado de una unidad de medida. Es el caso de masa, tiempo, temperatura, distancia. Por ejemplo, 5,5 kg, 2,7 s, 400 °C y 7,8 km, respectivamente.
Las vectoriales: Son aquellas que quedan totalmente definidas con un módulo, una dirección y un sentido. Es el caso de la fuerza, la velocidad, el desplazamiento. En estas magnitudes es necesario especificar hacia dónde se dirigen y, en algunos casos dónde se encuentran aplicadas. Todas las magnitudes vectoriales se representan gráficamente mediante vectores, que se simbolizan a través de una flecha.
Vector: Un vector tiene tres características esenciales: módulo, dirección y sentido. Para que dos vectores sean considerados iguales, deben tener igual módulo, igual dirección e igual sentido.
Los vectores se representan goemétricamente con flechas y se le asigna por lo general una letra que en su parte superior lleva una pequeña flecha de izquierda a derecha como se muestra en la figura 1.
Figura 1 Figura 2 Figura 3
Módulo: está representado por el tamaño del vector, y hace referencia a la intensidad de la magnitud ( número). Se denota con la letra solamente A o |A|
Dirección: corresponde a la inclinación de la recta, y representa al ángulo entre ella y un eje horizontal imaginario ( ver figura 2) . También se pueden utilizar los ejes de coordenadas cartesianas (x, y y z) como también los puntos cardinales para la dirección.
Sentido: está indicado por la punta de la flecha. (signo positivo que por lo general no se coloca, o un signo negativo). No corresponde comparar el sentido de dos vectores que no tienen la misma dirección, de modo que se habla solamente de vectores con el mismo sentido o con sentido opuesto.
Dirección: corresponde a la inclinación de la recta, y representa al ángulo entre ella y un eje horizontal imaginario ( ver figura 2) . También se pueden utilizar los ejes de coordenadas cartesianas (x, y y z) como también los puntos cardinales para la dirección.
Sentido: está indicado por la punta de la flecha. (signo positivo que por lo general no se coloca, o un signo negativo). No corresponde comparar el sentido de dos vectores que no tienen la misma dirección, de modo que se habla solamente de vectores con el mismo sentido o con sentido opuesto.
VECTORES EN EL PLANO CARTESIANO
- A un vector lo representamos gráficamente mediante un segmento orientado
- El módulo de un vector es su medida. Decimos que dos vectores tienen la misma dirección cuando están incluidos en la misma recta o en rectas paralelas.
- El sentido de un vector se indica gráficamente con la punta de la flecha.
- Dos vectores que tienen la misma dirección pueden tener el mismo sentido o sentidos opuestos.
- Dos vectores son opuestos cuando tienen la misma dirección, el mismo módulo y sentidos opuestos.
- Dos vectores son equipolentes si tienen el mismo módulo, la misma dirección y el mismo sentido.
- Para trabajar con vectores en el plano cartesiano, se elige como representante de todos los vectores equipolentes al que tiene origen en el punto (0;0) y se lo asocia a un par ordenado cuyas componentes son las coordenadas de su extremo
REPRESENTACIÓN GRÁFICA
Como los vectores tienen módulo y dirección, la suma de vectores no sigue las reglas de la suma tradicional de los escalares. De forma gráfica, la suma de dos vectores a→ y b→ nos dará como resultado otro vector c→ que podemos obtener mediante 2 métodos distintos: el método de la cabeza con cola (o del extremo con origen) y la regla del paralelogramo.
Método de la cabeza con cola.
Respetando la dirección y sentido de ambos vectores,
Desplazamos el vector b→ de tal forma que su origen se encuentre a continuación del extremo de a→.
c→ será el segmento recto que podamos dibujar desde el origen de a→ hasta el extremo de b→.
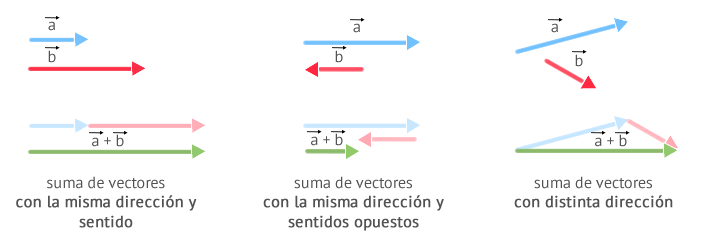
figura 6
REGLA DEL PARALELOGRAMO
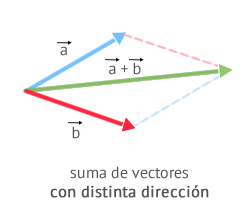
La podemos aplicar si los vectores no tienen la misma dirección:
Se situán los vectores a→ y b→ con los orígenes en el mismo punto
Desde el extremo de cada uno se dibuja una paralela al otro vector. Al final podremos ver un paralelogramo.
c→ será el vector que parte desde el origen común de a→ y b→ a través de la diagonal del paralelogramo.
Se situán los vectores a→ y b→ con los orígenes en el mismo punto
Desde el extremo de cada uno se dibuja una paralela al otro vector. Al final podremos ver un paralelogramo.
c→ será el vector que parte desde el origen común de a→ y b→ a través de la diagonal del paralelogramo.
SUMA DE VECTORES POR EL MÉTODO DE COMPONENTES
En este método analítico se descompone cada vector en dos componentes perpendiculares entre sí, según ilustraremos en el siguiente ejemplo. Sean nuevamente los vectores A, B y C del ejemplo anterior. El primer paso para sumar analíticamente estos tres vectores consiste en definir un sistema de coordenadas cartesianas, gracias al cual se especificará la dirección de cada vector. Ver la figura 8. Note que en este método todos los vectores se colocan con su extremo inicial en el origen
Se descompondrá cada uno de estos vectores en sus componentes horizontales y verticales. Para hacer esto considérese la figura 9. En esta figura se muestra el vector F localizado en un sistema coordenado cartesiano. La magnitud del vector es proporcional a la longitud de la flecha, mientras que su orientación está determinada por el ángulo θ que el vector hace con el lado positivo del eje x. Observar que el triángulo Oab es recto en el vértice a. El lado Oa es el cateto adyacente al ángulo q . El lado ab es opuesto al ánguloθ, y el segmento Ob es la hipotenusa del triángulo. El segmento ab es paralelo al eje y, y el cb, paralelo al eje x. Se ha designado como Fx al segmento Oa, Fy al ab, y F a la flecha Ob.
Por trigonometría elemental tenemos que, Fx = Fcosθ y Fy = Fsenθ, donde Fx y Fy se conocen como las componentes cartesianas del vector F. Ahora usaremos estas ecuaciones para encontrar las componentes de los vectores A, B y C. Los ángulos que estos vectores hacen con el lado positivo del eje x son 0º, 90º, y 225º, respectivamente. Recordemos que las magnitudes de A, B y C son 10 N, 15 N y 5 N respectivamente, entonces,
Ax = 10 cos 0º = 10 N, Bx = 15 cos 90º = 0
Ay = 10 sen 0º =0 , By = 15 sen 90º = 15 N
Cx = 5 cos 225º = -3.54 N, Cy = 5 sen 225º = -3.54 N
Las componentes a lo largo de cada eje pueden ahora ser tratadas como escalares. Se llamará Rx a la suma de las componentes en el eje x; y Ry a la suma de componentes en el eje y, es decir, Rx = Ax + Bx + Cx = (10 + 0 - 3.54) N = 6.46 N
Ry = Ay + By + Cy = (0 + 15 - 3.54) N = 11.46 N
La figura 10 muestra estas componentes y el nuevo vector R, al cual dan lugar. A partir de esta figura notamos que el ángulo θ puede deducirse mediante la función tangente como tan θ= Rx/Ry , mientras que la magnitud de R se obtiene con el teorema de Pitágoras.
Por otro lado:
REFERENCIAS:
- https://www.fisic.ch/contenidos/elementos-b%C3%A1sicos-1/vectores/
- https://www.fisicalab.com/apartado/suma-de-vectores#contenidos
- http://cdn.usc.edu.co/files/LABORATORIOS/GUIAS/CIENCIAS%20BASICAS/LABORATORIO%20PARA%20FISICA%20I/SUMA%20DE%20VECTORES.pdf
Comentarios
Publicar un comentario